目標：
這題主要目的在於介紹二元樹中最常見實用的類別：二元搜尋樹
(Binary Search Tree)

原題：

Question:
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
Both the left and right subtrees must also be binary search trees.

Example 1:
    2
   / \
  1   3
Input: [2,1,3]
Output: true

Example 2:
    5
   / \
  1   4
     / \
    3   6
Input: [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

分析/解題：
題目給定一個二元樹，檢查它是否是二元搜尋樹(Binary Search Tree)。
終於我們來到二元樹的進階版了！
二元搜尋樹如同題目說明，要符合以下三個特性：

1. 任一個節點的左子樹的所有節點值均小於該節點自身的值
2. 任一個節點的右子樹的所有節點值均大於該節點自身的值
3. 二元搜尋樹的左子樹和右子樹也都是二元搜尋樹

直觀來說，當我們從某個節點開始往左邊走的時候，一定要比自己小；
反之往右邊走的時候，要比自己大。也因為這個特性，當這棵樹足夠平衡時
(節點分布的很均勻時)，會相當有利於搜尋值，
因為每次都幾乎可以排除掉一半的可能性。

以下面的圖來說，我們想要從一個有15個節點的二元搜尋樹找到58這個值，
就要從根節點開始，每次比較大小，若58比較大就往右邊走，
比較小就往左邊走，直到找到剛好的值，或是碰到NIL(沒有別的節點可以搜尋)為止。

可以看到圖中由於深度一樣的關係，不論搜尋什麼值，
我們可以預期最多就只需要4次的比對就可以找出任意一個值是否在這棵樹裡面；
每次刪去一半的可能性，所以如果總節點有N個的話，
搜尋的複雜度最高即為O(logN)。

(記得我們提過二元樹不一定非得要全部都有連接節點，
這個結果是建立在這棵二元搜尋樹是**平衡(balanced)**的狀況，
如果這棵樹全部都改成只有左邊的節點的話，結果可是會變成O(N)的！)

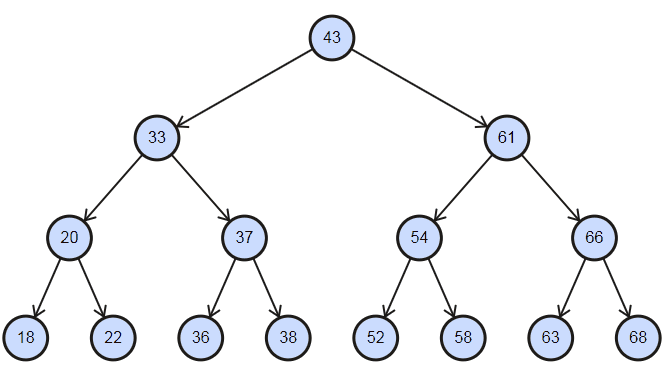
(Binary Serach Tree (Balanced, Complete, Perfect))

我們同樣以上面這棵樹為例，
如果我們想知道它從小到大的節點怎麼排序呢？
這裡就需要使用到In-order Traversal了。
In-order的順序為左-中-右，代表每次我們目標要先拿到左邊的值，
接著是中間，最後才是右邊的值；
我們最後希望拿到的是
[18, 20, 22, 33, 36, 37, 38, 43, 52, 54, 58, 61, 63, 66, 68]的話，
我們要先一路走到最左邊的節點，代表左邊沒有更小的值了，
才能將其印出來(18)，接著第二小的值則是最左邊節點的父節點(20)，
而對33來說，還有20的右節點22比它還要小，
最後以此類推，每次找到下一個最小值。
寫成虛擬碼如下：

inorder(root) {
  if root == NIL return
  inorder(root.left)
  print(root.val)
  inorder(root.right)
}

讀者可以嘗試使用上面的遞迴的方式走過一遍，相信會較為理解這整個流程。
留意上面由於當發現NIL的時候就直接return回到了遞迴的上一層，
所以就會造成類似往上走一層的效果。

回到我們的題目，我們已經知道在In-order的狀況下，
對於二元搜尋樹可以得到一個由小到大的順序，
所以只要記住上一個節點，每次去比較上一個節點和現在走到的節點，
當現在的節點跟上一個節點相比較小或相等時，
表示這不是二元搜尋樹(因為越後面的節點必須較大才行)；
反之，當每個節點都走完沒有錯誤時，
這時候就可以確認這個二元樹是二元搜尋樹了。

寫成虛擬碼如下：

let last = NIL
isValidBST(root) {
   if root == NIL return true
   if !isValidBST(root.left) return false
   if last != NIL and root.val <= last.val return false
   last = root // 更新上一個節點的位置
   return isValidBST(root.right)
}

Java的寫法部分，我們可以宣告一個class的變數last，
用來存放上一個走到的節點(放在函式內部的話會被洗掉)

Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    TreeNode last;
    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        if (!isValidBST(root.left)) return false;
        if (last != null && root.val <= last.val) return false;
        last = root;
        return isValidBST(root.right);
    }
}

Python的部分，請留意到記得在呼叫時使用self的關鍵字，
否則可能會無法在isValidBST中取得last。

Python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def __init__(self):
        self.last = None
    def isValidBST(self, root: TreeNode) -> bool:
        if not root: return True
        if not self.isValidBST(root.left): return False
        if self.last and root.val <= self.last.val: return False
        self.last = root
        return self.isValidBST(root.right)

面試實際可能會遇到的問題：
「時間/空間複雜度？」
（O(N), O(1)，因為要走過整個BST，
但除了幾個變數外，不需額外的資料結構）

「可否不用遞迴呢？」
(可以，使用Stack，可以用迴圈讓每次先將root塞入，一路向左邊走將每個左節點放入Stack中，接下來同樣每次取出一個節點，判斷和前一個的大小比較。最後每個左側處理完以後，再將位置移向右節點，迴圈重複即可。)

「可以不用class的變數來解此題嗎？」
(可以，有一種解法是記錄對某個節點的最小值和最大值限制，
將遞迴函式增加為傳入root, min, max，
並隨著每次看到的節點更新其底下的限制條件，
這樣就不需要按照in-order的方式移動，也不需要class的變數。
Java的解法這邊收錄 ryanswizzle在Leetcode的解法如下。)

public class Solution {
  public boolean isValidBST(TreeNode root) {
      return isValid(root, null, null);
  }

  public boolean isValid(TreeNode root, Integer min, Integer max) {
      if(root == null) return true;
      if(min != null && root.val <= min) return false;
      if(max != null && root.val >= max) return false;
    
      return isValid(root.left, min, root.val) && isValid(root.right, root.val, max);
  }
}

從LeetCode學演算法，我們下次見囉，掰~

下篇預告：
0094. Binary Tree Inorder Traversal (Medium)